Python 改进斐波那契数列递归后，计算第1000万项只需4秒

Python 改进斐波那契数列递归后，计算第1000万项只需4秒

改进思路

上一篇《不自己试试，还真猜不出递归函数的时间复杂度》中写了一个递归函数求斐波那契数列的某一项的值，号称它是终极改进了，但它有一个缺点：偶数项比奇数项算得慢。今天实然想到应该把偶数项也转换成奇数项来算，就会成倍提高运算速度：
 

原理是这样的：

F(2n)=F(n)*(F(n+1)+F(n-1)) ; F(2n+1)=F²(n+1)+F²(n)

偶数项需要三个项递归计算，奇数项只有两个项要递归。但是想到另外有公式可以把偶数项转换成奇数项：

∵ F(2n)=F(2n+1)-F(2n-1)

∴ F(2n)=F²(n+1)+F²(n) - (F²(n)+F²(n-1))=F²(n+1)-F²(n-1)

之前版本的时间测试，奇数项比偶数项计算快：

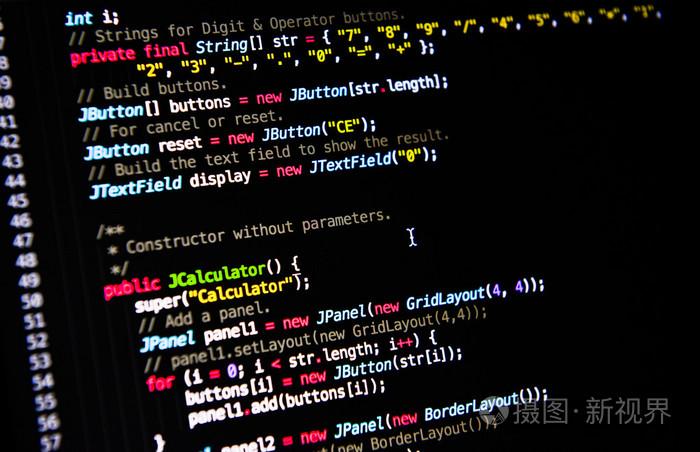
>>> def Fib(n:int,n1=34,n2=55):if n<11: return [0,1,1,2,3,5,8,13,21,34,55][n]if n==11: return n1+n2if n<1001:return Fib(n-1,n2,n1+n2)t=n//2if n%2: return Fib(t+1)**2+Fib(t)**2return Fib(t)*(Fib(t+1)+Fib(t-1))>>> for i in range(1,6):t=time();n=Fib(i*1000000);print(time()-t)t=time();n=Fib(i*1000000+1);print(time()-t)7.499995231628418
5.33894419670105
19.355664014816284
15.778117656707764
37.201030254364014
25.430164575576782>>> t=time();n=Fib(5000000);print(time()-t)
77.2153069972992
>>> t=time();n=Fib(5000000+1);print(time()-t)
53.111284017562866
>>>

改进一：偶数项改奇数项

>>> def Fib(n:int,n1=34,n2=55):if n<11: return [0,1,1,2,3,5,8,13,21,34,55][n]if n==11: return n1+n2if n<1001: return Fib(n-1,n2,n1+n2)t=n//2if n%2: return Fib(t+1)**2+Fib(t)**2return Fib(t+1)**2-Fib(t-1)**2>>> from time import time
>>> for i in range(1,7):t=time();n=Fib(i*1000000);print(f'Fib({i*1000000})::{time()-t}')t=time();n=Fib(i*1000000+1);print(f'Fib({i*1000000+1})::{time()-t}')Fib(1000000)::1.2499959468841553
Fib(1000001)::1.2343709468841553
Fib(2000000)::3.0624945163726807
Fib(2000001)::3.062493324279785
Fib(3000000)::5.203120470046997
Fib(3000001)::5.218744993209839
Fib(4000000)::7.812499523162842
Fib(4000001)::7.8281190395355225
Fib(5000000)::10.343748092651367
Fib(5000001)::10.343748331069946
Fib(6000000)::13.65624475479126
Fib(6000001)::13.671867370605469

用了新版公式后，不管奇数还是偶数项，耗时不再是起伏的而是单调递增且相邻的项用时基本相等，而且函数的运算速度也都成倍提高了。计算第500万项时，从原来的80秒减少到10秒了；计算第2000万项也只要80秒，而第1000万项只要半分钟就够了！

>>> from time import time
>>> t=time();n=Fib(10000000);print(time()-t)
27.9345383644104
>>> t=time();n=Fib(10000000+1);print(time()-t)
28.794012784957886
>>> t=time();n=Fib(20000000);print(time()-t)
77.22278428077698
>>> 

改进二：前面的项改用循环获取

把前面的项(比如前600项，具体定哪个值最优没有细测)用循环来获取，提速效果明显。

>>> def fib(n):if n<600:n1 = n2 = 1for _ in range(2,n):n1,n2 = n1+n2,n1return n1t = n//2if n%2: return fib(t+1)**2 + fib(t)**2else: return fib(t+1)**2 - fib(t-1)**2>>> t=time();n=fib(10000000);print(time()-t)
3.8922224044799805
>>> t=time();n=fib(10000001);print(time()-t)
3.8972229957580566
>>> t=time();n=fib(20000000);print(time()-t)
11.089634418487549
>>> t=time();n=fib(50000000);print(time()-t)
45.387596130371094
>>> 

计算第5000万项：45秒；第2000万项：11秒；第1000万项：4秒钟！ 

--All done!

附录

斐波那契数列重要恒等式

数列通项公式：
F(1)=F(2)=1;
F(n)=F(n-1)+F(n-2), n>2.

通项公式的前一项是：
F(n-1)=F(n-2)+F(n-3)
前一项代入通项中，得：
F(n)=2*F(n-2)+F(n-3)
再把更前一项F(n-2)=F(n-3)+F(n-4)代入上式，得：
F(n)=3*F(n-3)+2*F(n-4)
...以此类推：
F(n)=5*F(n-4)+3*F(n-5)
F(n)=8*F(n-5)+5*F(n-6)
F(n)=13*F(n-6)+8*F(n-7)
......
等号右边的系数又分别都是斐波那契数列，
两个新数列的函数自变量刚好差1，
且F(7)=13,F(6)=8，F(5)&#可得：

F(n)=F(m)F(n-m+1)+F(m-1)F(n-m) --公式①

先用m+n替换公式①中的n,得:

F(m+n)=F(m)*F(n+1)+F(m-1)*F(n) --公式②

令m=n,代入公式②,得:

F(2n)=F(n)*F(n+1)+F(n-1)*F(n) --公式③

再令m=n+1,代入公式②,得:
F(2n+1)=F(n+1)*F(n+1)+F(n)*F(n)
表示成平方和形式：

F(2n+1)=F²(n+1)+F²(n) --公式④

公式④自变量减一，得：

F(2n-1)=F²(n)+F²(n-1) --公式④'

公式④自变量增一，得：
F(2n+3)=F²(n+2)+F²(n+1)
上式与公式④相减：
F²(n+2)-F²(n)=F(2n+3)-F(2n+1)
而 F(2n+3)=F(2n+2)+F(2n+1)，所以：

F(2n+2)=F²(n+2)-F²(n) --公式⑤

还有一个公式：

F(n+1)*F(n-1)-F²(n)=(-1)ⁿ  --公式⑥