hdu 5116

hdu 5116

题目链接

 

Problem Description Matt loves letter L.

A point set P is (a, b)-L if and only if there exists x, y satisfying:

P = {(x, y), (x + 1, y), . . . , (x + a, y), (x, y + 1), . . . , (x, y + b)}(a, b ≥ 1)

A point set Q is good if and only if Q is an (a, b)-L set and gcd(a, b) = 1.

Matt is given a point set S. Please help him find the number of ordered pairs of sets (A, B) such that:

 

Input The first line contains only one integer T , which indicates the number of test cases.

For each test case, the first line contains an integer N (0 ≤ N ≤ 40000), indicating the size of the point set S.

Each of the following N lines contains two integers x _i, y _i, indicating the i-th point in S (1 ≤ x _i, y _i ≤ 200). It’s guaranteed that all (x _i, y _i) would be distinct.

 

Output For each test case, output a single line “Case #x: y”, where x is the case number (starting from 1) and y is the number of pairs.

 

Sample Input 2 6 1 1 1 2 2 1 3 3 3 4 4 3 9 1 1 1 2 1 3 2 1 2 2 2 3 3 1 3 2 3 3

 

Sample Output Case #1: 2 Case #2: 6 Hint n the second sample, the ordered pairs of sets Matt can choose are: A = {(1, 1), (1, 2), (1, 3), (2, 1)} and B = {(2, 2), (2, 3), (3, 2)} A = {(2, 2), (2, 3), (3, 2)} and B = {(1, 1), (1, 2), (1, 3), (2, 1)} A = {(1, 1), (1, 2), (2, 1), (3, 1)} and B = {(2, 2), (2, 3), (3, 2)} A = {(2, 2), (2, 3), (3, 2)} and B = {(1, 1), (1, 2), (2, 1), (3, 1)} A = {(1, 1), (1, 2), (2, 1)} and B = {(2, 2), (2, 3), (3, 2)} A = {(2, 2), (2, 3), (3, 2)} and B = {(1, 1), (1, 2), (2, 1)} Hence, the answer is 6. 题意：对于点集P 如果存在a,b使得P = {(x, y), (x + 1, y), . . . , (x + a, y), (x, y + 1), . . . , (x, y + b)}(a, b ≥ 1)，并且a，b互质，则P is good 。可以发现对于符合要求（good）的集合P ，其构成一个L 型，且以（x,y）为拐点，从（x,y）向上长度和向右长度 互质。现在给了N个点，求有多少对符合要求的L型集合不相交（集合交集为空）？ 思路：先找到所有符合要求的L个数S，那么用S*S-相交的L对数  即为结果。 怎么算相交的所有L对数呢？ 容斥，很妙的思想，遍历每一个点，如果当前的点是输入的点之一，那么是一个拐点，令这个拐点向右延伸最长为k，那么算出所有其它L的竖着部分与（x,y+k）相交的对数，乘以2，另外要考虑以（x,y）为拐点的L与自身相交的情况，把这两种相交情形减掉后既是结果。 代码如下：

#include <iostream>
#include <algorithm>
#include <cstdio>
#include <cstring>
using namespace std;
typedef long long LL;
const int N=40050;
const int M=205;
int R[M][M],U[M][M];
bool mp[M][M];
int dp[M][M],cnt[M][M];
int t[M][M];int gcd(int a,int b) { return (b==0)?a:gcd(b,a%b); }void init()
{for(int i=1;i<M;i++)for(int j=1;j<M;j++){dp[i][j]=dp[i][j-1]+((gcd(i,j)==1)?1:0);cnt[i][j]=cnt[i-1][j]+dp[i][j];}
}
int main()
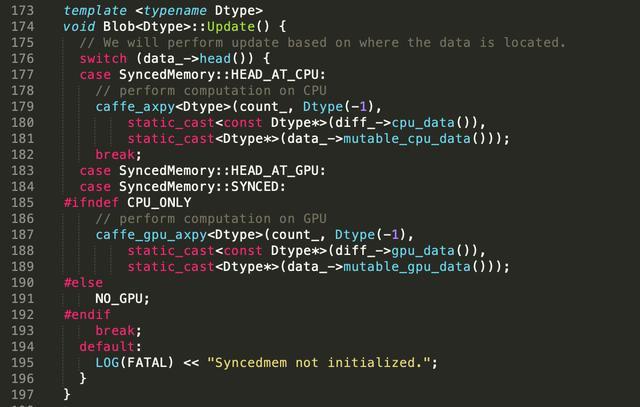
{init();int T,Case=1;cin>>T;while(T--){int n;  scanf("%d",&n);memset(mp,0,sizeof(mp));memset(U,0,sizeof(U));memset(R,0,sizeof(R));memset(t,0,sizeof(t));for(int i=1;i<=n;i++){int x,y;scanf("%d%d",&x,&y);mp[x][y]=1;}for(int i=200;i>=1;i--){for(int j=200;j>=1;j--){if(mp[i][j]){if(mp[i+1][j]) U[i][j]=U[i+1][j]+1;if(mp[i][j+1]) R[i][j]=R[i][j+1]+1;}}}LL s=0;for(int i=1;i<=200;i++){for(int j=1;j<=200;j++){if(mp[i][j]){s+=cnt[U[i][j]][R[i][j]];int d=0;for(int k=U[i][j];k>=0;k--){d+=dp[k][R[i][j]];t[i+k][j]+=d;}}}}LL ans=0;for(int i=1;i<=200;i++){for(int j=1;j<=200;j++){if(mp[i][j]){LL p=t[i][j];LL pp=cnt[U[i][j]][R[i][j]];p-=pp;for(int k=1;k<=R[i][j];k++){p+=t[i][j+k];ans+=2*p*dp[k][U[i][j]];}ans+=pp*pp;}}}s=s*s-ans;printf("Case #%d: %lldn",Case++,s);}return 0;
}

 

转载于:.html