数学表达式魔训day3

数学表达式魔训day3

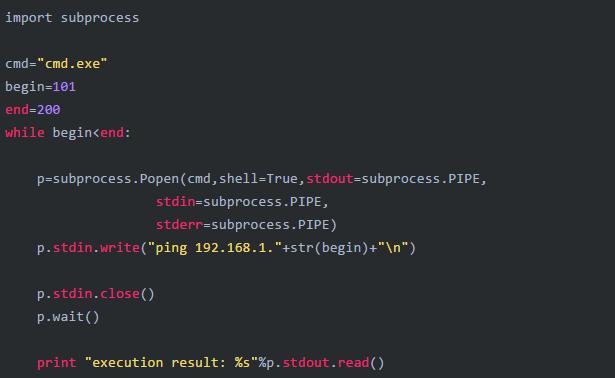
累加：
1. ∑ x i > 0 x i 2 sum_{x_i>0}x_i^2 ∑xi​>0​xi2​的 Java 代码怎么写?

double sum=0;
for(int i=0;i<n;i++)
{if(x[i]>0)sum+=x[i]*x[i];
}

2.将矩阵中小于 1 的分量平方并累加, 数学表达式如何和 Java 代码分别怎么写?

double sum=0;
for(i=0;i<n;i++)
{for(j=0;j<m;j++){if(x[i][j]<1)sum+=x[i][j]*x[i][j];}
}

定积分：
二重积分 ∫ 0 10 ∫ y 2 y 2 x 2 y + y 2 d x d y int_0^{10}int_{frac y 2}^y 2x^2y+y^2mathrm{d}xmathrm{d}y ∫010​∫2y​y​2x2y+y2dxdy
java代码：

double integration = 0;
double deltax = 0.01;
double deltay = 0.01;
for (double y = 0; y <= 10; y += delta)for (double x = y/2; x <= y; x += delta)integeration += (2 * x * x * y + y * y) * deltax * deltay;

作业：

1.将向量下标为偶数的分量 ( x 2 , x 4 , … ) (x_2,x_4,dots) (x2​,x4​,…) 累加, 写出相应表达式.

答： ∑ i m o d 2 = 0 n x i = ∑ i = 1 ⌊ n 2 ⌋ x 2 i sumlimits_{i mod 2 =0}^{n}x_{i}=sumlimits_{i=1}^{lfloor{frac n 2}rfloor}x_{2i} imod 2=0∑n​xi​=i=1∑⌊2n​⌋​x2i​
java代码：

double sum=0;
for(int i=1;i<=n;i++)
{if(i%2==0)sum+=x[i];
}

2.各出一道累加、累乘、积分表达式的习题, 并给出标准答案.

答： x = ( 1 , 8 , 4 , 2 , 5 ) mathbf{x}=(1,8,4,2,5) x=(1,8,4,2,5)
累加： ∑ i = 1 n x i = 1 + 8 + 4 + 2 + 5 = 20 sumlimits_{i=1}^{n}x_{i}=1+8+4+2+5=20 i=1∑n​xi​=1+8+4+2+5=20
累乘： ∏ i = 1 n x i = 1 × 8 × 4 × 2 × 5 = 320 prodlimits_{i=1}^{n}x_{i}=1times 8times 4times 2times 5=320 i=1∏n​xi​=1×8×4×2×5=320

定积分： ∫ 2 16 ∫ y + 4 3 y ( 4 x y + y 2 x + 2 x + y ) d x d y int_2^{16}int_{y+4}^{3y} (4xy+y^2x+2x+y)mathrm{d}xmathrm{d}y ∫216​∫y+43y​(4xy+y2x+2x+y)dxdy

double integration = 0;
double deltax = 0.01;
double deltay = 0.01;
for (int y = 2; y <= 16; y += delta)for (int x = y+4; x <= 3y; x += delta)integeration += (4 * x * y  + y * y*x+2*x+y) * deltax * deltay;

3.你使用过三重累加吗? 描述一下其应用.

答：三重累加应该可以用在多个矩阵与权重矩阵相乘再累加的时候。也可以说当多个矩阵累加时便可以用三重矩阵。
∑ i = 1 n ∑ j = 1 m x i j sumlimits_{i=1}^{n}sumlimits_{j=1}^{m}x_{ij} i=1∑n​j=1∑m​xij​这个算式计算 n × m ntimes m n×m阶矩阵各元素之和，是一个二重累加。若有k个矩阵， X 1 , X 2 , … , X k mathbf{X_1},mathbf{X_2},dots,mathbf{X_k} X1​,X2​,…,Xk​且都是 n × m ntimes m n×m阶矩阵，则计算所有矩阵元素之和则可以用三重累加。

4.给一个常用的定积分, 将手算结果与程序结果对比.

答： ∫ 3 6 ∫ 2 x 4 x 2 y d y d x int_3^{6}int_{2x}^{4x} 2ymathrm{d}ymathrm{d}x ∫36​∫2x4x​2ydydx

double integration = 0;double deltax = 0.001;double deltay = 0.001;for (double x = 3; x <= 6; x += deltax)for (double y = 2*x; y <= 4*x; y+= deltay)integration += (2*y) * deltax * deltay;

手算结果为：756.
∫ 3 6 ∫ 2 x 4 x 2 y d y d x = ∫ 3 6 12 x 2 d x = 4 x 3 ∣ 3 6 = 756 int_3^{6}int_{2x}^{4x} 2ymathrm{d}ymathrm{d}x=int_3^{6}12x^2mathrm{d}x=4x^3|_3^6=756 ∫36​∫2x4x​2ydydx=∫36​12x2dx=4x3∣36​=756
当 deltax = 0.001，deltay = 0.001时，程序计算结果为：755.87.

5.自己写一个小例子 ( n = 3 , m = 1 ) (n=3,m=1) (n=3,m=1) 来验证最小二乘法.

答：取 X = [ 5 , 16 , 24 ] mathbf{X}=[5,16,24] X=[5,16,24], Y = [ 4 , 17 , 24 ] mathbf{Y}=[4,17,24] Y=[4,17,24]
令 y = a 0 + a 1 × x y=a_0+a_1times x y=a0​+a1​×x
误差: ∑ i = j = 1 3 ( Y i − Y j ) 2 = ( 4 − a 0 − 5 a 1 ) 2 + ( 17 − a 0 − 5 a 1 ) 2 + ( 24 − a 0 − 24 a 1 ) sum limits_{i=j=1}^{3}(mathbf{Y}_i-mathbf{Y}_j)^2=(4-a_0-5a_1)^2+(17-a_0-5a_1)^2+(24-a_0-24a_1) i=j=1∑3​(Yi​−Yj​)2=(4−a0​−5a1​)2+(17−a0​−5a1​)2+(24−a0​−24a1​)
d d a 0 ∑ i = j = 1 3 ( Y i − Y j ) 2 = ⋯ = 0 frac d {da_0}sum limits_{i=j=1}^{3}(mathbf{Y}_i-mathbf{Y}_j)^2=dots=0 da0​d​i=j=1∑3​(Yi​−Yj​)2=⋯=0,得 3 a 0 + 45 a 1 = 45 3a_0+45a_1=45  3a0​+45a1​=45 (式1)
d d a 1 ∑ i = j = 1 3 ( Y i − Y j ) 2 = ⋯ = 0 frac d {da_1}sum limits_{i=j=1}^{3}(mathbf{Y}_i-mathbf{Y}_j)^2=dots=0 da1​d​i=j=1∑3​(Yi​−Yj​)2=⋯=0,得 45 a 0 + 857 a 1 = 868 45a_0+857a_1=868  45a0​+857a1​=868（式2）
由式1和式2得 a 0 = − 0.91 , a 1 = 1.06 a_0=-0.91,a_1=1.06 a0​=−0.91,a1​=1.06
所以得出线性关系为： y = 1.06 x − 0.91 y=1.06x-0.91 y=1.06x−0.91

6.自己推导一遍, 并描述这个方法的特点 (不少于 5 条).

答：自变量与超平面间的距离转化为概率 P ( y i ∣ x i ; w ) = 1 1 + e − x w P(y_i|x_i;mathbf{w})=frac 1 {1+e^{-mathbf{xw}}}  P(yi​∣xi​;w)=1+e−xw1​.
统一 y i y_i yi​得到 P ( y i ∣ x i ; w ) = P ( y i = 1 ∣ x i ; w ) y i ( 1 − P ( y i = 1 ∣ x i ; w ) ) 1 − y i P(y_i|x_i;mathbf{w})=P(y_i=1|x_i;mathbf{w})^{y_i}(1-P(y_i=1|x_i;mathbf{w}))^{1-y_i}    P(yi​∣xi​;w)=P(yi​=1∣xi​;w)yi​(1−P(yi​=1∣xi​;w))1−yi​ .
针对全部对象进行优化, 可将相应的概率相乘 (最大似然, maximal likelihood): arg ⁡ max ⁡ L ( w ) = ∏ i = 1 n P ( y i ∣ x i ; w ) arg max L(mathbf{w}) =prodlimits_{i=1}^{n}P(y_i|x_i;mathbf{w}) argmaxL(w)=i=1∏n​P(yi​∣xi​;w)
取对数方便计算，不改变单调性：
log ⁡ L ( w ) = ∑ i = 1 n log ⁡ P ( y i ∣ x i ; w ) log L(mathbf{w})=sumlimits_{i=1}^{n}log P(y_i|x_i;mathbf{w}) logL(w)=i=1∑n​logP(yi​∣xi​;w)
= ∑ i = 1 n y i log ⁡ P ( y i = 1 ∣ x i ; w ) + ( 1 − y i ) log ⁡ ( 1 − P ( y i = 1 ∣ x i ; w ) ) =sumlimits_{i=1}^{n}y_ilog P(y_i=1|x_i;mathbf{w})+(1-y_i)log (1-P(y_i=1|x_i;mathbf{w})) =i=1∑n​yi​logP(yi​=1∣xi​;w)+(1−yi​)log(1−P(yi​=1∣xi​;w))
= ∑ i = 1 n y i log ⁡ P ( y i = 1 ∣ x i ; w ) 1 − P ( y i = 1 ∣ x i ; w ) + log ⁡ ( 1 − P ( y i = 1 ∣ x i ; w ) ) =sumlimits_{i=1}^{n}y_ilog frac {P(y_i=1|x_i;mathbf{w})} {1-P(y_i=1|x_i;mathbf{w})}+log (1-P(y_i=1|x_i;mathbf{w})) =i=1∑n​yi​log1−P(yi​=1∣xi​;w)P(yi​=1∣xi​;w)​+log(1−P(yi​=1∣xi​;w))
= ∑ i = 1 n y i x i w − log ⁡ ( 1 + e x i w ) =sumlimits_{i=1}^{n}y_i mathbf{x}_i mathbf{w}-log (1+ e^{mathbf{x}_i mathbf{w}}) =i=1∑n​yi​xi​w−log(1+exi​w)
对 w mathbf{w} w求偏导
log ⁡ L ( w ) ∂ w = ∑ i = 1 n y i x i − e x i w 1 + x i w x i frac{log L(mathbf{w})} {partial mathbf{w}}=sumlimits_{i=1}^{n}y_imathbf{x}_i-frac{e^{mathbf{x}_imathbf{w}}}{1+mathbf{x}_imathbf{w}}mathbf{x}_i ∂wlogL(w)​=i=1∑n​yi​xi​−1+xi​wexi​w​xi​
= ∑ i = 1 n ( y i − e x i w 1 + x i w ) x i =sumlimits_{i=1}^{n} left (y_i-frac{e^{mathbf{x}_imathbf{w}}}{1+mathbf{x}_imathbf{w}} right) mathbf{x}_i =i=1∑n​(yi​−1+xi​wexi​w​)xi​
用梯度下降求解
w t + 1 = w t − α log ⁡ L ( w ) ∂ w mathbf{w}^{t+1}=mathbf{w}^t-alpha frac{log L(mathbf{w})} {partial mathbf{w}} wt+1=wt−α∂wlogL(w)​
特点：

• 在 m 维空间上,m维向量 w mathbf{w} w确定了一条直线. 为方便起见, 令 w mathbf{w} w 为列向量. 点 x mathbf{x} x 与 w mathbf{w} w 的距离为 x w mathbf{x}mathbf{w} xw.
• logistic回归的因变量可以是二分类的，也可以是多分类的.
• 如果正确分类, 则离超平面越远越好; 如果错误分类, 则离超平面越近越好.
• 使用 sigmoid 函数(常用)将自变量到超平面的距离转成 (我们以为的) 概率.
• 概率 P ( y i ∣ x i ; w ) = P ( y i = 1 ∣ x i ; w ) y i ( 1 − P ( y i = 1 ∣ x i ; w ) ) 1 − y i P(y_i|x_i;mathbf{w})=P(y_i=1|x_i;mathbf{w})^{y_i}(1-P(y_i=1|x_i;mathbf{w}))^{1-y_i}    P(yi​∣xi​;w)=P(yi​=1∣xi​;w)yi​(1−P(yi​=1∣xi​;w))1−yi​ 将 y i = 1 y_i=1 yi​=1和 y i = 0 y_i=0 yi​=0都包含到式子.
• 对 w mathbf{w} w求偏导，令其为0，无法获得解析式，所以用梯度下降法求.