华为2019年4月10号春招实习机试

华为2019年4月10号春招实习机试

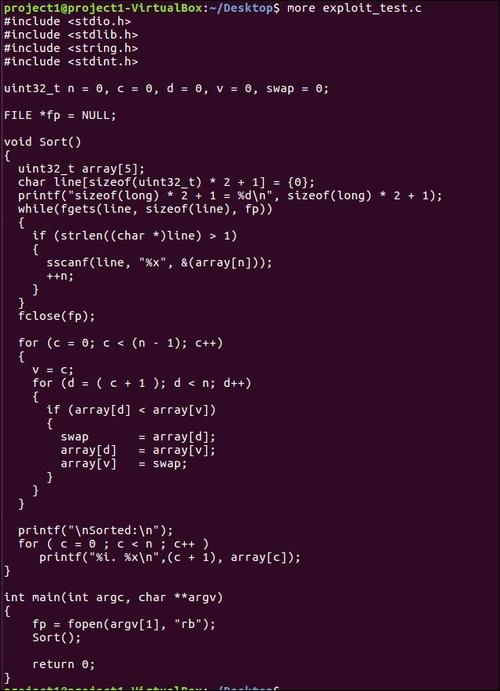
第一题：

package huawei;import java.util.*;/*** 题目描述：连续输入字符串，以空格键分割，输入字符串个数为n，* 请按长度为8拆分每个字符串后输出新的字符串数组，输出的字符串按照升序排列。* 长度不是8整数的在后面补0，空字符串不处理。第一个输入的字符串为个数n，后面的为n个待处理的字符串。* 测试用例：* <p>* 输入：* 2 abc 1234567890* 1* <p>* 输出：* 12345678 90000000 abc00000*/
public class HWCode1 {public static void main(String[] args) {Scanner sc = new Scanner(System.in);int n = sc.nextInt();String[] strs = sc.nextLine().trim().split(" ");sc.close();List<String> list = new ArrayList<String>();for (String str : strs) {StringBuffer sb = new StringBuffer(str);if ((str.length() & 7) != 0) {sb.append("0000000");}while (sb.length() > 7) {list.add(sb.substring(0, 8));sb = sb.delete(0, 8);}}Collections.sort(list);for (int i = 0; i < list.size(); i++) {System.out.(i)+" ");}}
}

第二题：

package huawei;import java.util.Scanner;/*** 题目描述：给定一个字符串，字符串包含数字、大小写字母以及括号（包括大括号，中括号，小括号），括号可以嵌套，即括号里面可以出现数字和括号。* 按照如下规则对字符串进行展开，不需要考虑括号不成对的问题，不考虑数字后面没有括号的情况，即 2a2(b)不考虑。* 数字表示括号里的字符串重复的次数，展开后的字符串不包含括号* 将字符串进行逆序展开* 测试用例：* <p>* 输入：* abc3(A)* 1* <p>* 输出：* AAAcba*/
public class HWCode2 {public static void main(String[] args) {Scanner sc = new Scanner(System.in);String str = sc.nextLine();sc.close();System.out.println(new StringBuffer(process(str, 1)).reverse());}private static String process(String str, int repeatTimes) {if (repeatTimes == 0) return "";StringBuffer res = new StringBuffer();int newRepeatTimes = 0;for (int i = 0; i < str.length(); i++) {char curChar = str.charAt(i);if (curChar >= '0' && curChar <= '9') {newRepeatTimes = Integer.valueOf(curChar) - 48;} else if (curChar == '{' || curChar == '[' || curChar == '(') {int end = i + 1;if (curChar == '{') {end = str.indexOf('}', i);} else if (curChar == '[') {end = str.indexOf(']', i);} else {end = str.indexOf(')', i);}res.append(process(str.substring(i + 1, end), newRepeatTimes));i = end;} else {res.append(curChar);}}String tempStr = String();for (int i = 1; i < repeatTimes; i++) {res.append(tempStr);}String();}
}

第三题：

取余10^9不会，这个暴力递归必超时

package huawei;import java.util.Scanner;/*** 题目描述：在N*M的地图上，每个点的海拔不同，从当前位置只能访问上下左右四个点且是没有访问过的点，此外下一步选择的点的海拔必须大于当前点。* 求从点A到点B一共有多少条路径，输出路数总数取余10^9* 左上角的坐标为（0,0），右下角的坐标为（N-1,M-1）* 测试用例：* <p>* 输入：第一行为地图大小，下面n行为每个点的海拔，最后一行前两个为A坐标（x,y）,后两个为B坐标（z,v）* 4 5* 0 1 0 0 0* 0 2 3 0 0* 0 0 4 5 0* 0 0 7 6 0* 0 1 3 2* <p>* 输出：* 2*/
public class HWCode3 {public static void main(String[] args) {Scanner sc = new Scanner(System.in);int n = sc.nextInt();int m = sc.nextInt();int[][] M = new int[n][m];for (int i = 0; i < n; i++) {for (int j = 0; j < m; j++) {M[i][j] = sc.nextInt();}}int x = sc.nextInt();int y = sc.nextInt();int z = sc.nextInt();int v = sc.nextInt();sc.close();if (z >= n || z < 0 || v >= m || v < 0) System.out.println(0);else System.out.println(findPath(M, n, m, x, y, z, v));}private static int findPath(int[][] M, int n, int m, int x, int y, int z, int v) {// 如果A点在M内，才能找到路径，且能向上下左右四个方向寻址if (x < n && x >= 0 && y < m && y >= 0) {// base case:如果A点和B点重合，即认为是一条路径if (x == z && y == v) return 1 & (1000000000 - 1);// 递归int left = 0, right = 0, up = 0, down = 0;if (x > 0 && M[x - 1][y] > M[x][y]) { // 能向左走left = findPath(M, n, m, x - 1, y, z, v);}if (x < n - 1 && M[x + 1][y] > M[x][y]) { // 能向右走right = findPath(M, n, m, x + 1, y, z, v);}if (y > 0 && M[x][y - 1] > M[x][y]) { // 能向上走up = findPath(M, n, m, x, y - 1, z, v);}if (y < m - 1 && M[x][y + 1] > M[x][y]) { // 能向下走down = findPath(M, n, m, x, y + 1, z, v);}return left + right + up + down;}// 不在M内则返回0；return 0;}
}