冒泡排序及算法优化

冒泡排序及算法优化

基本思想：比喻很形象，就像轻的气泡向上冒，重的气泡往下沉，依次比较两个数，将小的放前面，大的放后面。举个例子，对于n个无序的数列，在第一趟比较第0个数和第1个数将较下的数放前面，较大的数放后面，然后比较第1个数和第2个数，小的放前面，大的放后面，一直继续下去直到比较最后两个数，第一趟比较结束后，数列中最后一个数就是无序数列中最大的数。第二趟，继续从第0个数和第1个数开始比较，小数放前，大数放后，一直比较到倒数第二个数（倒数第一个数已经是最大的了），第二趟比较结束，倒数第二个数即是数列中第二大的数，依次内推，重复以上步骤，直到n-1趟比较排序完成。

时间复杂度：O(n*n)

空间复杂度：O(1)

是否是稳定排序：稳定排序

代码示例：

#include <stdio.h>
#include <stdlib.h>#define SIZE 10int Swap(int *a, int *b)
{int c;int ret = -1;ret = (a != NULL)&&(b != NULL);if(ret){c = *a;*a = *b;*b = c;}return ret;
}int BubbleSort1(int a[], int n)
{int i = 0, j = 0;int ret = -1;ret = (a != NULL)&&(n > 0);if(ret){for(i = 0; i < n; i++){for(j = 0; j < n - i -1; j++){if(a[j] > a[j+1]){Swap(&a[j], &a[j+1]);}}}}return ret;	
}int PlayFunc(int *a, int n)
{int i = 0;int ret = -1;ret = (a != NULL)&&(n > 0);if(ret){printf("Array[]:");for(i = 0; i < n; i++)printf("%d, ", a[i]);printf("n");}return ret;
}void main(void)
{int array[SIZE] = {8,5,10,7,6,9,4,3,2,1};PlayFunc(array, 10);BubbleSort1(array, 10);PlayFunc(array, 10);} 

运行效果截图：

根据上面的编程思想不难写出上面的代码，毕竟是最简单的入门级排序算法。下面是对算法优化了一点的，网上已经有众多大神写过了，记得大学时第一次看到人家优化的这个算法，真是相当佩服！虽然不难，但能想到也不容易。

基本思想：就是设置一个标志位，这个标志位用来标志某一趟排序比较中是否发生了交换，如果本趟没有发生任何数据交换，则表示整个排序已经完成。为了突出优化后的效果，对程序做了小小的改动。但还是一样的配方，还是原来的味道。

示例代码：(程序比较简单就不加注释了)

#include <stdio.h>
#include <stdlib.h>#define SIZE 10int exchange_times = 0;
int compare_times = 0;int Swap(int *a, int *b)
{int c;int ret = -1;ret = (a != NULL)&&(b != NULL);if(ret){c = *a;*a = *b;*b = c;}return ret;
}int BubbleSort1(int a[], int n)
{int i = 0, j = 0;int ret = -1;ret = (a != NULL)&&(n > 0);if(ret){for(i = 0; i < n; i++){for(j = 0; j < n - i -1; j++){if(a[j] > a[j+1]){Swap(&a[j], &a[j+1]);exchange_times++;}compare_times++;}}}return ret;	
}int BubbleSort2(int a[], int n)
{int i = 0, j = 0;int ret = -1;int flag = 1;ret = (a != NULL)&&(n > 0);if(ret){for(i = 0; (i < n)&&flag; i++){flag = 0;for(j = 0; j < n - i -1; j++){if(a[j] > a[j+1]){Swap(&a[j], &a[j+1]);flag = 1;exchange_times++;}compare_times++;}	}}return ret;		
}int PlayFunc(int *a, int n)
{int i = 0;int ret = -1;ret = (a != NULL)&&(n > 0);if(ret){printf("Array[]:");for(i = 0; i < n; i++)printf("%d, ", a[i]);printf("n");}return ret;
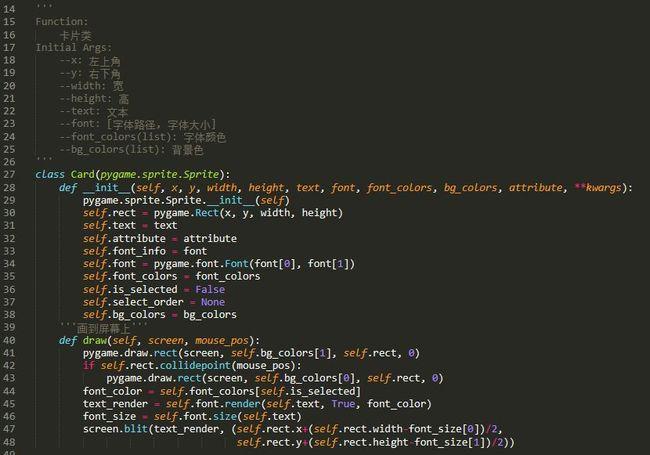
}void main(void)
{//int array[SIZE] = {8,5,10,7,6,9,4,3,2,1};int array[SIZE] = {10,1,2,3,4,5,6,7,8,9,};PlayFunc(array, 10);//BubbleSort1(array, 10);BubbleSort2(array, 10);PlayFunc(array, 10);printf("exchange_times: %dn", exchange_times);printf("compare_times: %dn", compare_times);} 

为了突出优化后的优势(对数组元素做了小改动)，分别打印出BubbleSort1和BubbleSort2排序过程中的比较次数和数组元素交换的次数。

BubbleSort2运行截图：

BubbleSort1运行截图：

可以看到同样的无序数组，优化后的比较次数比优化之前的少多了。上面的代码算是之前学了了别人的然后今天自己要把学过数据结构和算法好好总结一下，好歹还是自己徒手一个一个敲出来的。

冒泡排序还能继续优化，记得之前也是在CSDN别人的博客上看到的吧！实在是大神！前面两种之前都研究过，只是刚学时老忘，后来学到一定程度，发现一般只要理清了算法的思路，都能把代码撸出来。

优化的假设场景：如果有N个数的数组，仅仅前面一小部分无序，后面大部分都是有序的且有序部分均大于前面小部分的无序部分，假设N = i + j,0到i是无序部分，i+1到j是有序部分。且i+1到j之间的元素都大于0到i之间的元素。按照上面的第一趟冒泡排序结束后，最后发生数组元素交换的位置肯定不超过i,即第一趟发生交换后0到i这一部分最大的数据出来了，而这个最大的数据小于后边所有有序元素数据。所以记录下这个位置(这个位置后边的数据都已经有序了)，下一趟冒泡排序只需要遍历到该位置即可。这算是集前面两个优点于一身，就是变量稍微多了两个。

代码例程：

int BubbleSort3(int a[], int n)
{int i = 0, j = 0;int ret = -1;int flag = 1;int point = n;//用于记录位置 ret = (a != NULL)&&(n > 0);if(ret){for(i = 0; (i < point)&&flag; i++){flag = 0;point = n;for(j = 0; j < point - i -1; j++){if(a[j] > a[j+1]){Swap(&a[j], &a[j+1]);flag = 1;n = j + 2;//记录第一趟最后交换位置 exchange_times++;}compare_times++;}	}}return ret;		
}

测试的main函数：

void main(void)
{	//int array[SIZE] = {8,5,10,7,6,9,4,3,2,1};//int array[SIZE] = {10,1,2,3,4,5,6,7,8,9};int array[SIZE] = {4,1,3,2,5,6,7,8,9,10};PlayFunc(array, 10);//BubbleSort1(array, 10);//BubbleSort2(array, 10);BubbleSort3(array, 10);PlayFunc(array, 10);printf("exchange_times: %dn", exchange_times);printf("compare_times: %dn", compare_times);	
}

数组稍微作了一点改动，前面4个无序后面6个有序且前面4个均小于后面6个元素

BubbleSort1运行截图：

BubbleSort2运行截图：

BubbleSort3运行截图：

自己一个字一个字的码博客好费时间，今天算是温故而知新吧！