hdu3982 Harry Potter and J.K.Rowling（半平面交 + 圆与多边形求交）

hdu3982 Harry Potter and J.K.Rowling（半平面交 + 圆与多边形求交）

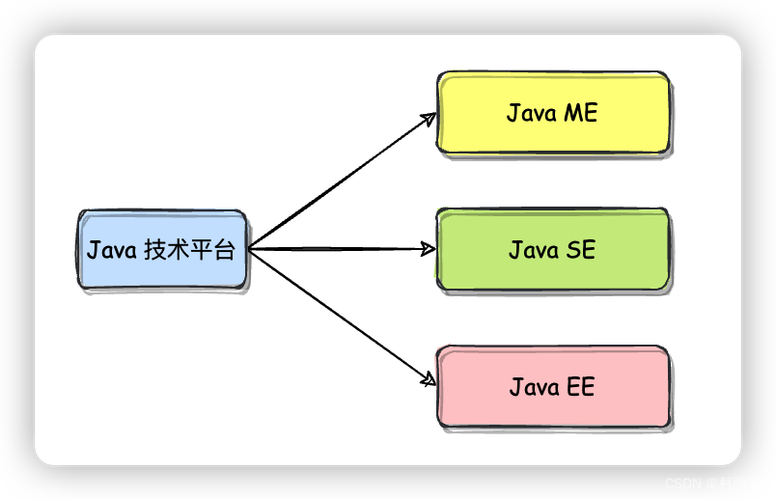
题目意思：有一块半径为r的圆形蛋糕，其中心在原点，有一个人在某一个点（x，y），

现把蛋糕按两点所在直线切蛋糕，求切了n次后，这个人所在蛋糕的面积占总面积的百分比。

代码如下：

//140MS
#include<iostream>
#include<cstdio>
#include<math.h>
#define eps 1e-8
#define maxn 10000
#define PI acos(-1.0)
struct point{double x,y;};
point p[maxn],save[maxn],temp[maxn];
point points[maxn][2];
point cen,people;
int n,ns,m;
double r;
double xmult(point p1,point p2,point p0)
{return (p1.x-p0.x)*(p2.y-p0.y)-(p1.y-p0.y)*(p2.x-p0.x);
}
double dmult(point p1,point p2,point p0)
{return (p1.x-p0.x)*(p2.x-p0.x)+(p1.y-p0.y)*(p2.y-p0.y);
}
double distance(point p1,point p2)
{return sqrt((p1.x-p2.x)*(p1.x-p2.x)+(p1.y-p2.y)*(p1.y-p2.y));
}
void mycopy(point *s,int &ns,point *temp,int n)
{int i;ns=n;for(i=0;i<n;i++)s[i]=temp[i];
}
void getline(point p1,point p2,double &a,double &b,double &c)
{a=p2.y-p1.y;b=p1.x-p2.x;c=p2.x*p1.y-p1.x*p2.y;
}
point intersection(point p1,point p2,point p3,point p4)
{point ret=p1;double t=((p1.x-p3.x)*(p3.y-p4.y)-(p1.y-p3.y)*(p3.x-p4.x))/((p1.x-p2.x)*(p3.y-p4.y)-(p1.y-p2.y)*(p3.x-p4.x));ret.x+=(p2.x-p1.x)*t;ret.y+=(p2.y-p1.y)*t;return ret;
}
void cut(point side)
{int i,j;temp[0].x=-10000;temp[0].y=-10000;temp[1].x=-10000;temp[1].y=10000;temp[2].x=10000;temp[2].y=10000;temp[3].x=10000;temp[3].y=-10000;ns=m=4;for(i=0;i<n;i++){double a,b,c;if(xmult(side,points[i][1],points[i][0])>=0)getline(points[i][0],points[i][1],a,b,c);else  getline(points[i][1],points[i][0],a,b,c);int cnt=0;for(j=0;j<ns;j++){if(a* temp[j].x+b* temp[j].y+c>=0){save[cnt++]=temp[j];}else{point p1=temp[(j-1+ns)%ns],p2=temp[(j+1)%ns];if(a*p1.x+b*p1.y+c>0)save[cnt++]=intersection(points[i][0],points[i][1],p1,temp[j]);if(a*p2.x+b*p2.y+c>0)save[cnt++]=intersection(points[i][0],points[i][1],p2,temp[j]);}}mycopy(temp,ns,save,cnt);}
}
double cirtri(point pa,point pb,point po,double r)
{double a,b,c,x,y;double area=xmult(pa,pb,po)/2;a=distance(po,pb);b=distance(po,pa);c=distance(pa,pb);if(a<=r&&b<=r)//1{return area;}else if(a<r&&b>=r)//2{x=(dmult(pa,po,pb)+sqrt(c*c*r*r-xmult(pa,po,pb)*xmult(pa,po,pb)))/c;return asin(area*(c-x)*2/c/b/r)*r*r/2+area*x/c;}else if(a>=r&&b<r)//3{y=(dmult(pb,po,pa)+sqrt(c*c*r*r-xmult(pb,po,pa)*xmult(pb,po,pa)))/c;return asin(area*(c-y)*2/c/a/r)*r*r/2+area*y/c;}else if(fabs(2*area)>=r*c||dmult(pb,po,pa)<=0||dmult(pa,po,pb)<=0)//4{if(dmult(pa,pb,po)<0){if(xmult(pa,pb,po)<0){return (-PI-asin(area*2/a/b))*r*r/2;}else return (PI-asin(area*2/a/b))*r*r/2;}else return asin(area*2/a/b)*r*r/2;}else //5{x=(dmult(pa,po,pb)+sqrt(c*c*r*r-xmult(pa,po,pb)*xmult(pa,po,pb)))/c;y=(dmult(pb,po,pa)+sqrt(c*c*r*r-xmult(pb,po,pa)*xmult(pb,po,pa)))/c;return (asin(area*(1-x/c)*2/r/b)+asin(area*(1-y/c)*2/r/a))*r*r/2+area*((y+x)/c-1);}
}
int main()
{int cas;scanf("%d",&cas);int i,j,k;for(k=1;k<=cas;k++){scanf("%lf%d",&r,&n);for(i=0;i<n;i++)scanf("%lf%lf%lf%lf",&points[i][0].x,&points[i][0].y,&points[i][1].x,&points[i][1].y);scanf("%lf%lf",&people.x,&people.y);cut(people);double res=0;cen.x=0;cen.y=0;for(i=0;i<ns;i++)res+=cirtri(save[i],save[(i+1)%ns],cen,r);double ans=fabs(100.0*res)/(PI*r*r);printf("Case %d: %.5lf%%n",k,ans);}return 0;
}